Elastic Potential Energy Calculator
What is an Elastic Potential Energy Calculator?
An Elastic Potential Energy Calculator is a tool that calculates the energy stored in a stretched or compressed elastic object, like a spring or rubber band. This type of energy is stored when an object is deformed (stretched or compressed) and is released when it returns to its normal shape. The formula to calculate elastic potential energy is:
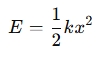
where:
- E is the elastic potential energy (in joules, J),
- k is the spring constant (in N/m, Newtons per meter),
- x is the displacement or deformation (in meters, m).
Why use an Elastic Potential Energy Calculator?
- Saves time and simplifies calculations: Instead of manually plugging values into the formula, you can instantly get the result.
- Ensures accuracy: Reduces the risk of errors when calculating energy in various applications.
- Important for physics and engineering: Helps in understanding and designing systems with springs, rubber bands, or other elastic materials.
- Useful in energy conversion studies: Shows how potential energy is stored and can later be converted to kinetic energy or work.
How does it work?
The calculator takes two key inputs:
- Spring constant (k): This value represents the stiffness of the spring and is often determined experimentally or provided for a specific material.
- Displacement (x): This is how far the spring is stretched or compressed from its equilibrium (rest) position.
Using the formula 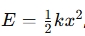 , the calculator computes the amount of energy stored.
, the calculator computes the amount of energy stored.
Example Calculation:
If a spring has a spring constant k=200 N/m, and it is stretched by x=0.1 m, the elastic potential energy stored in the spring would be:
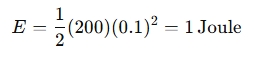
When to use an Elastic Potential Energy Calculator?
- In physics experiments to calculate the energy stored in springs or other elastic materials.
- In engineering applications such as designing shock absorbers, spring-loaded mechanisms, or devices that rely on elastic deformation.
- In biomechanics when analyzing energy stored in muscles, tendons, or other elastic structures in the body.
- In construction and material science to analyze stress and strain in materials under deformation.