Lens Maker Equation Calculator

Enter value and click on calculate. Result will be displayed.
Select calculator :
 
Satellite Mean Orbital Radius (r) :
Planet Mass (M) :
Result:

A Lens Maker Equation Calculator is a tool used to calculate the focal length of a lens given certain parameters like the refractive index and the radii of curvature of the lens surfaces. The Lens Maker's Equation is an essential formula in optics that relates the focal length of a lens to these characteristics, helping you understand how the lens will bend light and its optical power.

Why use a Lens Maker Equation Calculator?

The Lens Maker's Equation is particularly useful in designing optical systems (like eyeglasses, microscopes, telescopes, and cameras) where precise control over focal lengths is required. This calculator helps to:

  • Simplify calculations: It automates the process of solving the lens maker equation, saving time and reducing human errors.
  • Understand lens properties: It provides a clearer understanding of how different lens properties (like curvature and refractive index) affect the lens's focal length.
  • Design lenses accurately: For optical engineers, scientists, and anyone working with lenses, it's important to know how to calculate focal lengths to achieve the desired imaging or magnification effects.

How does a Lens Maker Equation Calculator work?

The Lens Maker's Equation relates the focal length f of a lens to its refractive index nn n, and the radii of curvature of the two surfaces R1​ and R2​ . The equation is:

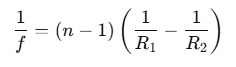
Where:

  • f is the focal length of the lens,
  • n is the refractive index of the material of the lens (dimensionless),
  • R1 is the radius of curvature of the first surface (positive if convex, negative if concave),
  • R2 is the radius of curvature of the second surface (positive if convex, negative if concave).

To use the calculator, you simply input:

  • The refractive index nn n,
  • The radii of curvature R1​ and R2​ .

The calculator then computes the focal length of the lens.

When to use a Lens Maker Equation Calculator?

  • Designing optical systems: When designing lenses for cameras, microscopes, telescopes, or corrective lenses (like eyeglasses), you’ll need to calculate the focal length to understand how the lens will focus light.
  • Understanding lens behavior: In physics and optics, the calculator is used to quickly determine the behavior of light passing through different types of lenses.
  • Precision lens manufacturing: In industrial applications, where lenses need to be manufactured with exact specifications, this equation helps in determining the necessary curvature and material to achieve the desired focal length.
  • Educational purposes: For students studying optics or anyone learning how light interacts with lenses, the calculator can be a helpful tool to visualize and solve problems.

Example

Suppose we have a lens with:

  • Refractive index n=1.5,
  • Radius of curvature of the first surface R1=10 cm,
  • Radius of curvature of the second surface R2=−15 cm.

So, the focal length of the lens is 12 cm.

More Complex Example

In some cases, lenses may have asymmetrical shapes (such as cylindrical lenses), or you may need to account for thicker lenses. In these cases, the calculation could involve more complex variations of the Lens Maker's Equation, but the basic idea is the same. The calculator can handle these more complex scenarios, depending on the model.