Perpendicular Length Calculator (Distance)

Enter value and click on calculate. Result will be displayed.
X1 :
Y1 :
A :
B :
C :
Result:
Length of Perpendicular :

A Perpendicular Length (Distance) Calculator is a tool used to calculate the shortest distance between a point and a line or plane in geometry. This is often referred to as the perpendicular distance, and it's crucial in various fields like geometry, physics, engineering, and computer graphics.

What is Perpendicular Length (Distance)?
The perpendicular distance is the shortest distance from a point to a line or from a point to a plane. It forms a right angle (90°) with the line or plane, meaning the point lies directly above or below the line/plane along the shortest path.

For example:

  • Point to Line: The perpendicular distance from a point (x1,y1) to a line Ax+By+C=0 is given by:
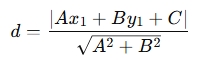
  • Point to Plane: For a point P(x1,y1,z1) and a plane Ax+By+Cz+D=0, the perpendicular distance is:

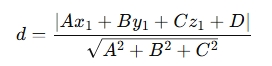
Why use a Perpendicular Length (Distance) Calculator?

  • Saves Time: Quickly computes the shortest distance without complex calculations.
  • Improves Accuracy: Reduces errors in geometric problems, especially with non-obvious angles or 3D spaces.
  • Simplifies Geometry: Helps in solving problems that involve angles, projections, and distances.
  • Useful in Various Fields: Applies to physics, engineering, computer graphics, architecture, and more.

How does a Perpendicular Length (Distance) Calculator work?

  • Input:
    • Coordinates of the point and the equation of the line (or plane).
    • For point to line: You provide the coordinates of the point and the coefficients A,B,C from the line equation.
    • For point to plane: You provide the point’s coordinates and the coefficients A,B,C,D from the plane equation.
  • Calculation: The calculator applies the respective formula to compute the perpendicular distance.
  • Output: The shortest distance between the point and the line/plane (in units of length).

When should you use a Perpendicular Length (Distance) Calculator?

  • In geometry problems: Calculating distances between points and lines, or points and planes.
  • In physics: Determining the shortest distance between an object and a surface, especially in optics or mechanics.
  • In engineering: For designing structures and understanding how components fit relative to each other.
  • For computer graphics: Calculating distances in 3D space, such as the distance between a point and a surface.
  • In navigation: To determine the shortest path between a point and a fixed line (e.g., for aerial navigation or road routes).