Physical Pendulum Calculator
A Physical Pendulum Calculator is a tool used to calculate the period of oscillation of a physical (compound) pendulum — an object that swings back and forth around a fixed pivot point, where its mass is distributed along its length (unlike a simple pendulum, which assumes all mass is concentrated at a point).
What is a Physical Pendulum?
A physical pendulum is a rigid body that swings under the influence of gravity, where the mass is not concentrated at one point but spread across the object’s shape and size. Examples include:
- A swinging rod fixed at one end
- A door rotating on its hinges
- A swinging disc or plate
The period of oscillation (T) for a physical pendulum is given by:
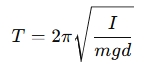
Where:
- T = Period of oscillation (time for one complete swing)
- I = Moment of inertia of the pendulum around the pivot (kg·m²)
- m = Mass of the pendulum (kg)
- g = Acceleration due to gravity (9.81 m/s² on Earth)
- d = Distance from the pivot point to the pendulum’s center of mass (m)
Why use a Physical Pendulum Calculator?
- Saves Time: Quickly determines the period without lengthy calculations.
- Ensures Accuracy: Reduces human error in complex formulas.
- Engineering Applications: Used in designing mechanical systems involving oscillations.
- Educational Tool: Helps students understand pendulum motion in physics.
How does a Physical Pendulum Calculator work?
- Input:
- Mass of the object (m)
- Moment of inertia (I)
- Distance from the pivot to the center of mass (d)
- Gravitational acceleration (optional — typically 9.81 m/s2)
- Calculation: Uses the formula for the period of a physical pendulum.
- Output: Period of oscillation (T), usually in seconds.
When should you use a Physical Pendulum Calculator?
- In physics experiments: Studying the motion of physical pendulums.
- For mechanical design: Calculating oscillation periods in machinery.
- In clock-making: Designing pendulum clocks with accurate timing.
- For structural analysis: Studying swinging behavior of suspended objects.