Product to Sum Trigonometry Identities Calculator
What is a Product to Sum Trigonometry Identities Calculator?
A Product to Sum Trigonometry Identities Calculator is a tool that converts expressions involving products of trigonometric functions (such as sine and cosine) into sums of trigonometric functions. This tool uses product-to-sum identities, which are useful for simplifying complex trigonometric expressions. The key product-to-sum identities are:
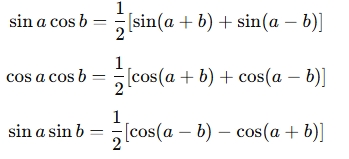
These identities are helpful in simplifying the analysis of trigonometric functions, especially in calculus and physics.
Why use a Product to Sum Trigonometry Identities Calculator?
- Simplification: It helps reduce the complexity of trigonometric expressions, making them easier to work with.
- Integration and differentiation: Product-to-sum identities are often used in calculus to simplify the integration or differentiation of trigonometric functions.
- Solving trigonometric equations: The calculator makes it easier to manipulate and solve equations involving trigonometric products.
- Fourier transforms and signal processing: In physics and engineering, these identities are used to convert products of sinusoids into sums, which simplifies signal analysis.
- Identities verification: It helps in verifying trigonometric identities or converting them into an equivalent form for easier understanding.
How does a Product to Sum Trigonometry Identities Calculator work?
- Input: The product of two trigonometric functions, such as sin a cos b, cos a cos b, or sin a sin b.
- Select identity: Choose the appropriate product-to-sum identity based on the input.
- Apply the identity: The calculator automatically applies the corresponding identity to convert the product into a sum or difference.
- Output: A simplified expression that involves sums or differences of trigonometric functions.
For example:
If you have sin30∘cos45∘, you can use the identity:
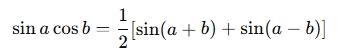
Applying it:
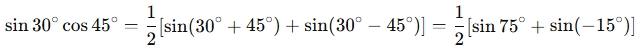
When is a Product to Sum Trigonometry Identities Calculator used?
- In calculus: To simplify integrals and derivatives of trigonometric functions.
- In signal processing: When analyzing or manipulating waves and signals in Fourier analysis.
- In physics: To simplify expressions for wave interference and resonance.
- In trigonometry classes: To convert between different forms of trigonometric functions for easier problem-solving.
- In engineering: For electrical engineering and circuit analysis involving sinusoidal signals.