Rectangular to Polar Conversion Calculator
A Rectangular to Polar Conversion Calculator is a tool that converts coordinates from the rectangular (Cartesian) system — where points are defined by x- and y-coordinates — to the polar coordinate system, where points are defined by radius and angle.
Why use a Rectangular to Polar Conversion Calculator?
- Simplifies Complex Numbers: Polar coordinates make it easier to work with complex numbers, trigonometry, and vector math.
- Useful in Physics and Engineering: Many physical systems (like waves, circular motion, and electromagnetic fields) are easier to describe in polar form.
- Easier Calculations for Rotation and Scaling: Polar coordinates simplify transformations like rotation and scaling.
- Graphing Circular Patterns: When working with curves and shapes like circles and spirals, polar coordinates are often more intuitive.
How does a Rectangular to Polar Conversion Calculator work?
The calculator uses these formulas to convert the Cartesian coordinates (x, y) into polar coordinates (r,θ):
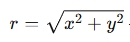 — the distance from the origin (0, 0) to the point
— the distance from the origin (0, 0) to the point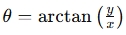 — the angle from the positive x-axis to the point (in radians or degrees)
— the angle from the positive x-axis to the point (in radians or degrees)
Input:
- x-coordinate
- y-coordinate
Calculation: It computes the radius rr r and the angle θ.
Output:
- r: The distance from the origin to the point
- θ: The angle in degrees or radians
When should you use a Rectangular to Polar Conversion Calculator?
- In Trigonometry and Calculus: When working with curves and integrals in polar form.
- For Electrical Engineering: Analyzing AC circuits often involves phasors, which use polar representation.
- In Computer Graphics: Rotations and scaling transformations can be more efficient in polar form.
- For Navigation and Robotics: Polar coordinates make sense for systems based on angles and distances from a fixed point.