Simple Pendulum Calculator

Enter value and click on calculate. Result will be displayed.
Select calculator:
 
Length (l):
m
Acceleration of Gravity (ag):
m/s
Result:

A Simple Pendulum Calculator is a tool used to calculate the characteristics of a simple pendulum, such as its period (the time it takes to complete one full swing) or length based on given parameters. A simple pendulum is a weight (or bob) attached to the end of a string or rod that swings back and forth under the influence of gravity, typically with small angular displacements.

Why Simple Pendulum Calculator is used:

It’s used because:

  • Physics and engineering applications: The simple pendulum is a model that helps understand periodic motion, oscillations, and forces like gravity.
  • Time measurement: Pendulums are used in clocks (historically) to measure time accurately.
  • Educational purposes: In physics, it’s a fundamental example for learning about harmonic motion, forces, and energy conservation.
  • Mechanical systems: Pendulums are also used in systems like metronomes, clocks, and some types of sensors.

How Simple Pendulum Calculator works:

The main parameter that can be calculated for a simple pendulum is its period T, which is the time it takes to complete one full oscillation (from one extreme to the other and back).

The formula for the period T of a simple pendulum is:

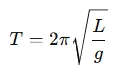
Where:

  • T is the period (in seconds).
  • L is the length of the pendulum (in meters).
  • g is the acceleration due to gravity (approximately 9.81 m/s² on Earth).
  • π is approximately 3.14159.

If you know the length L of the pendulum and the acceleration due to gravity gg g, the calculator can compute the period. Conversely, if you know the period, you can rearrange the formula to solve for L:

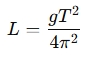
The calculator can also be used to find other parameters related to the pendulum's motion, such as its angular frequency or maximum speed, depending on the input values.

When to use Simple Pendulum Calculator:

You would use this calculator when:

  • Studying harmonic motion: To understand how objects oscillate under the influence of restoring forces, often used in introductory physics courses.
  • Timekeeping and clocks: In designing or understanding the workings of mechanical clocks or pendulum-based timing devices.
  • Engineering applications: When dealing with mechanical oscillators or sensors that rely on pendulum-like motion.
  • Experimentation and measurement: When conducting experiments related to gravitational acceleration or the dynamics of oscillating systems.

For example, if you're working on a project where you need to design a pendulum clock, this calculator will help you determine the length of the pendulum required to achieve a desired period or frequency of oscillation.