Square Pyramidal Number Calculator

Enter value and click on calculate. Result will be displayed.
Non-Negative Number (n):
Result:
Square Pyramidal Number (Pn):

A Square Pyramidal Number Calculator is a tool used to calculate Square Pyramidal Numbers for a given n, where n is the number of levels or layers in the pyramid. A Square Pyramidal Number represents the total number of stacked squares in a 3D pyramid with a square base, where each layer is a square number (i.e., the number of squares in the base decreases as you move up each level).

Why Square Pyramidal Number Calculator is used:

The calculator is used because Square Pyramidal Numbers arise in different areas of mathematics and combinatorics, especially when studying stacking or triangular pyramids with square bases. It is helpful for:

  • Mathematics and number theory: Square pyramidal numbers are an interesting sequence studied in algebra and combinatorics.
  • Geometric modeling: In applications that require calculating or visualizing 3D pyramid-like structures.
  • Combinatorics and counting: When dealing with problems that involve counting objects arranged in a square pyramid pattern.

How Square Pyramidal Number Calculator works:

A Square Pyramidal Number for a given n (where n is the number of layers) is calculated using the following formula:

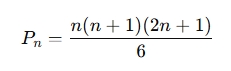
Where:

  • Pn​ is the nth square pyramidal number.
  • n is the number of layers (or the position in the series of square pyramidal numbers).

This formula sums the squares of the first nn n natural numbers to get the total number of stacked squares (or units) in the pyramid.

When to use Square Pyramidal Number Calculator:

You would use this calculator in situations like:

  • Mathematical problems: In problems where you need to find or work with square pyramidal numbers, such as in combinatorics or sequence analysis.
  • Geometric design: When modeling or analyzing 3D pyramid-like structures, especially when they have a square base.
  • 3D visualization: In fields like computer graphics or architecture, where understanding the number of objects in a pyramidal stack can be useful.
  • Counting and optimization: In problems where you're counting stacked objects or analyzing how objects are arranged in a square pyramid shape.

For example, if you wanted to know how many total squares are in a square pyramid with 4 layers, you would input n=4 into the calculator, and it would return the value for P4​ . This is useful in both theoretical and practical applications where patterns and arrangements are important.