Sum of a Linear Number Sequence Calculator

Enter value and click on calculate. Result will be displayed.
Select calculator:

Enter total number of terms (nth term):
Enter the first term (a):
Enter the common difference (d):
Result:
Sequence:
Nth term value:
Sum of all terms upto term:

A Sum of a Linear Number Sequence Calculator is a tool used to calculate the sum of a sequence of numbers that follows a linear pattern, typically an arithmetic sequence. An arithmetic sequence is a sequence of numbers where the difference between consecutive terms is constant.

Why Sum of a Linear Number Sequence Calculator is used:

It’s used because calculating the sum of such sequences by hand can be time-consuming, especially when the sequence has many terms. This calculator simplifies the process and provides quick, accurate results. It's especially useful in:

  • Mathematics and statistics: For problems involving arithmetic series or sequences.
  • Finance: To calculate the total amount of payments or returns over time (e.g., annuities).
  • Engineering and computer science: For algorithm analysis, or when solving for sums in linear systems or simulations.

How Sum of a Linear Number Sequence Calculator works:

The sum of the first nn n terms in an arithmetic sequence can be calculated using the formula:

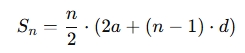
Where:

  • Sn​ is the sum of the first nn n terms.
  • a is the first term in the sequence.
  • d is the common difference (the amount by which each term increases or decreases).
  • n is the number of terms.

Alternatively, the sum can also be expressed as:

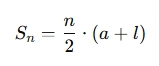
Where:

  • l is the last term in the sequence.

You input the first term, common difference, and the number of terms into the calculator, and it computes the sum for you.

When to use Sum of a Linear Number Sequence Calculator:

You would use this calculator when:

  • Solving math problems: In algebra, calculus, or number theory, where you need to calculate the sum of an arithmetic series.
  • Finance calculations: To find the sum of payments or investments that increase or decrease linearly over time (like monthly payments on a loan or savings).
  • Engineering problems: When the problem involves a linear progression of quantities or measurements.
  • Data analysis: For analyzing trends or sequences in data that follow a linear pattern.

For example, if you're trying to calculate the total sum of a sequence of numbers like 5, 8, 11, 14, ... (with a common difference of 3), this calculator will instantly give you the sum of the first nn n terms without you having to manually add each term.