T-Test Calculator - T-Distribution Critical Values Table

What is a T-Test Calculator?
A T-Test Calculator is a statistical tool that helps determine if there’s a significant difference between the means of two groups. It’s based on the t-distribution, a probability distribution used when sample sizes are small, and the population standard deviation is unknown.

There are three main types of t-tests:

• One-sample t-test: Compares the sample mean to a known or hypothesized population mean.
• Two-sample t-test: Compares the means of two independent groups.
• Paired t-test: Compares means from the same group at two different times (before and after a treatment).

Why use a T-Test Calculator?

• Simplifies calculations: Avoids doing complex formulas by hand.
• Reduces human error: Ensures accurate results for statistical analysis.
• Determines significance: Helps assess whether observed differences are likely due to chance.
• Widely used: Essential in research, business, and medical studies.

How does a T-Test Calculator work?

• Input:
  • Sample means
  • Standard deviations
  • Sample sizes
  • Significance level (like 0.05)
• Calculation:
  1. Computes the t-statistic:
     
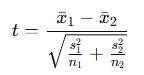
  2. Compares the t-statistic to critical values from the t-distribution table.
  3. Determines p-value and whether the result is statistically significant.

T-Distribution Critical Values Table:
The t-distribution table provides critical values based on:

• Degrees of freedom (df): df = n − 1 for one sample, or based on a more complex formula for two samples.
• Significance level (α): Common values are 0.05 (5%) or 0.01 (1%).
• Tails of the test: One-tailed or two-tailed tests.

When to use a T-Test Calculator?

• Comparing test scores: Checking if one class performed better than another.
• Evaluating treatments: Seeing if a new drug has a significant effect compared to a placebo.
• Business decisions: Comparing customer satisfaction before and after a policy change.
• Scientific research: Testing hypotheses with small sample sizes.