Damped Oscillation Calculator

Undamped angular frequency (ω0)=
Drag coefficient(k)=
Initial displacement(x0)=
Repetition frequency=
 

What is a Damped Oscillation Calculator?

A Damped Oscillation Calculator is a tool that helps analyze oscillatory motion in systems where the amplitude of the oscillations decreases over time due to friction, resistance, or other dissipative forces. This phenomenon is called damping, and it is common in mechanical systems (like springs), electrical circuits, and even in acoustic or seismic applications.

In a damped oscillation, the system experiences a gradual reduction in energy, causing the oscillations to fade until the object comes to rest or reaches equilibrium.

Why Use a Damped Oscillation Calculator?

  • Study of oscillatory systems: Helps understand and predict the behavior of damped harmonic oscillators in mechanical and electrical systems.
  • Design and analysis of systems: Used in designing systems like shock absorbers, suspension systems, or RLC (resistor-inductor-capacitor) circuits.
  • Predict motion characteristics: Predict the decay rate of oscillations and how quickly a system loses energy.
  • Optimize energy efficiency: Analyze damping in systems to minimize energy losses, vibrations, or resonance issues.

How to Calculate Damped Oscillation?

Damped oscillations are described by the following equation:

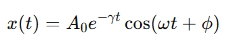
Where:

  • x(t) = Displacement at time t
  • A0​ = Initial amplitude (maximum displacement)
  • γ = Damping coefficient (describes how quickly the oscillations decay)
  • ω = Angular frequency (related to the natural frequency of the system)
  • t = Time
  • ϕ = Phase constant (initial phase of oscillation)

The damping coefficient γ and angular frequencyω are related to the damping type:

  • Underdamped system: Oscillations occur, but their amplitude decreases over time.
  • Critically damped system: The system returns to equilibrium without oscillating.
  • Overdamped system: The system slowly returns to equilibrium without oscillating, but slower than in the critically damped case.

The key parameters involved are:

  1. Natural frequency ​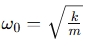 (where k is the spring constant, and m is the mass of the object).
  2. Damping coefficient 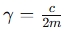(where c is the damping constant).

When to Use a Damped Oscillation Calculator?

  • Engineering and design: When designing suspension systems, shock absorbers, or mechanical systems that need to handle vibrations.
  • Electrical circuits: In analyzing RLC circuits, where damping affects signal quality and resonance behavior.
  • Physics and mechanics: Studying the effects of damping on harmonic oscillators (like a mass on a spring).
  • Seismology: Analyzing vibrations or seismic waves, where damping is critical in reducing building or ground oscillations.
  • Noise reduction: Designing systems to reduce oscillations in machinery, such as motors, to minimize noise and vibration.