Compound Pendulum (Physical Pendulum) Calculator
A Compound Pendulum (Physical Pendulum) Calculator is a tool used to calculate the period of oscillation for a compound (or physical) pendulum. Unlike a simple pendulum, which consists of a mass at the end of a string or rod, a compound pendulum consists of a rigid body with its mass distributed along its length, which causes more complex motion. The body swings around a pivot point, and the moment of inertia must be considered when calculating the period of oscillation.
Why is it important?
- Complex Motion: Unlike a simple pendulum, a compound pendulum has mass distributed over its length, so the motion is more complex and requires consideration of the distribution of mass.
- Practical Applications: Compound pendulums are used in various applications such as in clocks (where a rigid body like a wheel or disk swings), seismometers, and in mechanical systems that involve rotational motion.
- Engineering and Design: Understanding the behavior of compound pendulums is important in designing systems with oscillating parts, like suspension systems, machinery, or instruments with oscillating components.
- Physics Education: A compound pendulum is a useful example in physics classes for studying rotational motion, moments of inertia, and forces acting on rigid bodies.
How is it calculated?
The period of oscillation of a compound pendulum is determined using the following formula:
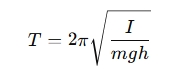
Where:
- T is the period of the pendulum (in seconds, s),
- I is the moment of inertia of the pendulum about the pivot point (in kg·m²),
- m is the mass of the pendulum (in kilograms, kg),
- g is the acceleration due to gravity (approximately 9.81 m/s2 on Earth),
- h is the distance from the pivot point to the center of mass of the pendulum (in meters, m).
When is it used?
A Compound Pendulum (Physical Pendulum) Calculator is used in various scenarios:
- Physics Problems: In education, to calculate the period and behavior of compound pendulums in simple harmonic motion, helping to demonstrate the effects of mass distribution and moments of inertia.
- Mechanical Clocks: In the design of mechanical clocks, where the pendulum might be a rigid body (like a wheel or disk) swinging back and forth to regulate time.
- Engineering: In engineering applications where oscillating systems involve rigid bodies with distributed mass, such as in suspension systems, vibration analysis, or mechanical designs.
- Seismology: In the design of seismographs, where a compound pendulum might be used to detect and measure the intensity of seismic waves based on its oscillation.
In summary:
A Compound Pendulum (Physical Pendulum) Calculator helps calculate the period of oscillation for systems where the mass is distributed along a rigid body and the object swings around a pivot point. It is crucial for understanding rotational motion, moments of inertia, and for applications in clocks, mechanical systems, and physics education. By accounting for the mass distribution, this calculator provides insights into more complex oscillatory motion beyond simple pendulums.