Quantum_harmonic_oscillator
What is a Quantum Harmonic Oscillator?
A Quantum Harmonic Oscillator (QHO) is a fundamental model in quantum mechanics that describes a particle subject to a restoring force proportional to its displacement, similar to a classical mass-spring system but governed by quantum laws. It is one of the few quantum systems with an exact analytical solution.
Why is the Quantum Harmonic Oscillator Important?
- Foundation of Quantum Mechanics – Many quantum systems approximate a harmonic oscillator, including atoms, molecules, and solid-state physics.
- Energy Quantization – The QHO naturally leads to discrete energy levels, explaining quantum behavior.
- Wavefunction Solutions – The eigenfunctions are Hermite polynomials multiplied by a Gaussian, crucial in quantum chemistry and physics.
- Models Vibrations in Molecules – Used to describe molecular vibrations, phonons in solids, and even quantum field modes.
How Does the Quantum Harmonic Oscillator Work?
The Schrödinger equation for a 1D harmonic oscillator is:
Key Quantum Features of the QHO
- Energy Quantization: Unlike the classical oscillator, a quantum oscillator has discrete energy levels.
- Zero-Point Energy: The lowest energy state (n=0) has energy
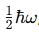, meaning the particle never truly stops moving. - Wavefunctions (ψn(x)): Solutions are expressed in terms of Hermite polynomials multiplied by a Gaussian envelope.
- Uncertainty Principle: The minimum uncertainty product ΔxΔp=ℏ / 2 is achieved in the ground state.
When is the Quantum Harmonic Oscillator Used?
- Quantum Chemistry & Molecular Physics – Models vibrational spectra of molecules.
- Solid-State Physics – Describes phonons, which are quantized lattice vibrations in crystals.
- Quantum Optics – Helps in understanding coherent states of light.
- Quantum Field Theory – Forms the basis of quantized fields and particle physics.