Pendulum Calculator
A Pendulum Calculator is a tool used to calculate the period, frequency, and other properties of a simple pendulum. A pendulum consists of a mass (called a bob) suspended from a fixed point and is allowed to swing freely back and forth. The movement of the pendulum is governed by gravity and its length.
Why is it important?
- Understanding Oscillatory Motion: The pendulum is a classic example of simple harmonic motion, which is fundamental in physics for understanding periodic and oscillatory systems.
- Applications in Clocks: Pendulums were historically used in mechanical clocks to maintain accurate time.
- Engineering and Design: Pendulum-like systems are used in engineering applications that involve oscillations, such as in seismic sensors, balancing systems, or even in the design of some musical instruments.
- Physics Education: Pendulums are often used in physics classrooms to demonstrate the principles of motion, energy conservation, and gravitational forces.
How is it calculated?
For a simple pendulum, the period (time it takes to complete one full swing) is calculated using the formula:
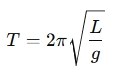
Where:
- T is the period of the pendulum (in seconds, s),
- L is the length of the pendulum (in meters, m),
- g is the acceleration due to gravity (approximately 9.81 m/s2on Earth).
For small oscillations (where the angle of swing is small), the period is independent of the mass of the bob and only depends on the length of the pendulum and the acceleration due to gravity. This relationship is an approximation that works for small angles of deflection.
When is it used?
A Pendulum Calculator is useful in several scenarios, including:
- Physics Problems: In education, to calculate the period and behavior of pendulums in simple harmonic motion, for experiments and problem-solving.
- Clocks and Timekeeping: In the design of mechanical clocks, pendulums are often used to regulate time by maintaining a steady, consistent period of oscillation.
- Seismology and Engineering: Pendulum-based devices can be used to measure small changes in motion or vibrations, such as in seismographs or other sensors.
- Oscillating Systems: Pendulum-like motion is important in engineering designs where periodic motion is needed, such as in some suspension systems or in the design of certain musical instruments.
In summary:
A Pendulum Calculator helps calculate the period, frequency, and other properties of a pendulum's motion. It’s vital for understanding oscillatory motion, used in physics education, mechanical timekeeping, and engineering applications. By providing insights into the behavior of pendulums, it can also be applied to various practical and theoretical problems involving harmonic motion.