Speed of sound calculator

What is a Speed of Sound Calculator?

A speed of sound calculator is a tool used to determine the speed at which sound waves travel through a given medium (air, water, metal, etc.). The speed of sound varies based on the medium's properties, such as temperature, pressure, and density.

For air at a given temperature, the speed of sound (c) can be approximated using the formula:

c = 331.3 + 0.6T

Where:

c = Speed of sound in air (m/s)
T = Temperature in degrees Celsius (°C)

For any medium, a more general formula is:

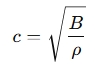
Where:

B = Bulk modulus (elasticity) of the medium (Pa)
ρ = Density of the medium (kg/m³)

Why Use a Speed of Sound Calculator?

Physics & Acoustics: Understanding wave propagation in different materials.
Aerospace & Aviation: Calculating Mach numbers for supersonic flight.
Engineering & Materials Science: Evaluating structural integrity using ultrasonic testing.
Meteorology: Measuring atmospheric conditions affecting sound travel.
Marine & Submarine Navigation: Sonar calculations for underwater communication.

How to Use the Calculator?

For air:
- Enter the temperature in °C.
- Use c=331.3+0.6T to get the speed in m/s.
For other media:
- Obtain the bulk modulus (B) and density (ρ) of the material.
- Use c=√B/ρ to calculate the speed.
For gases (ideal gas approximation):

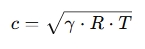
Where:
- γ = Adiabatic index (1.4 for air)
- R = Specific gas constant (287 J/kg·K for air)
- T = Absolute temperature in Kelvin (K)

When is the Speed of Sound Calculation Used?

In aviation and space exploration: To determine aircraft speed relative to Mach 1.
In medical imaging: Used in ultrasound diagnostics.
For underwater acoustics: Sonar systems for submarines and marine research.
In material science: Evaluating mechanical properties using ultrasonic testing.
For weather prediction: Studying temperature effects on sound propagation in the atmosphere.